Skip to main content

Compound expressions

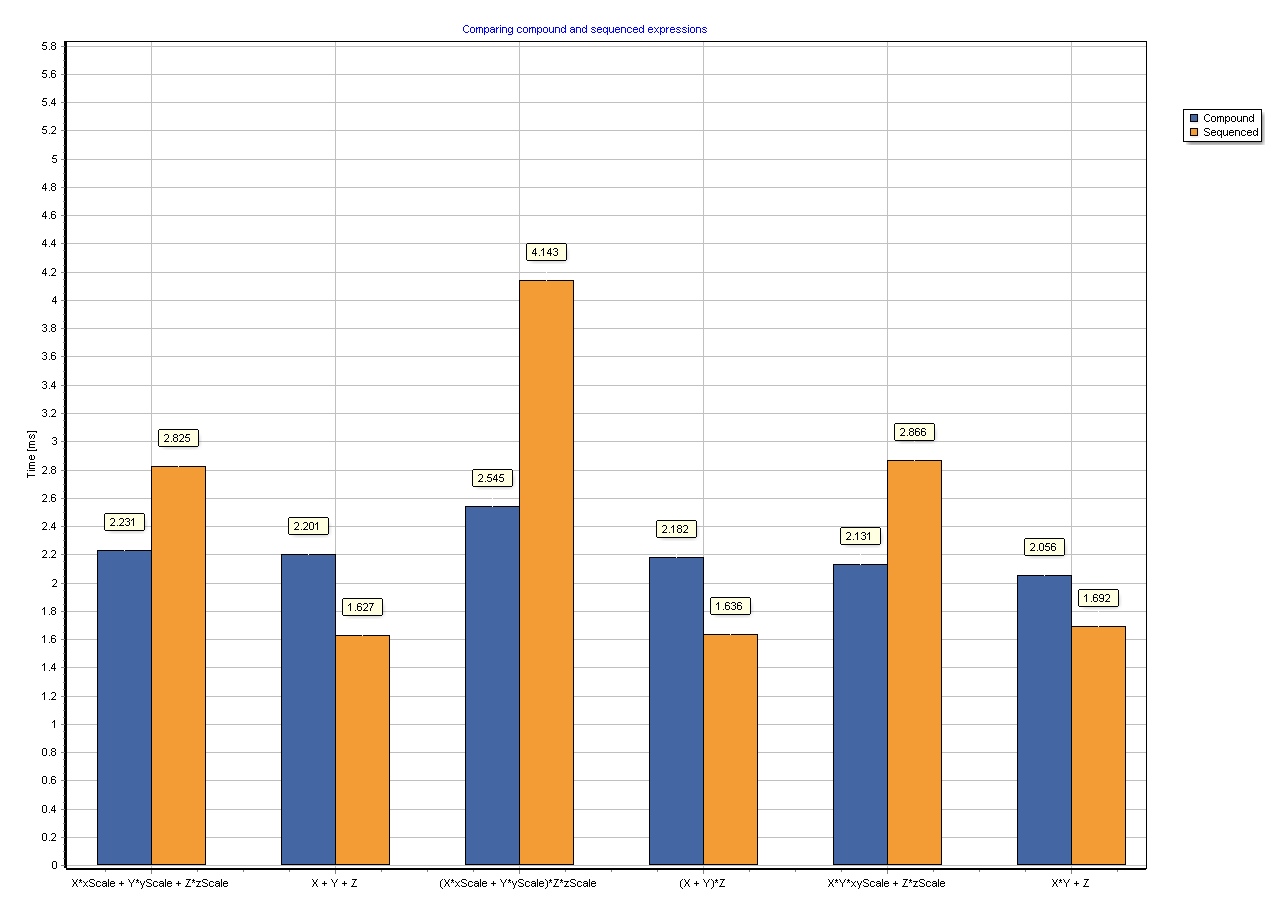
When vectorizing the code it is beneficial, if we can do more than one vectorizable operation in the same loop. Especially it makes sense to do such operations, which do not require additional memory bandwidth. The CPUs vectorization is much more powerfull computationally, than it is typically possible to feed to it from the memory even if cached. While the CPU is waiting for the next value from the memory, this time can be used for some additionall math, which will not slow down the primary operation. Welcome to the MtxVec "compound expressions". Over 160 overloads have been added to TMtxVec type from which both TVec and TMtx derive to address this possibility. Below you can see an example from MtxVec Demo when executed on AMD Zen 2 (Rome) architecture at 3,2Ghz. Orange are sequenced expressions using Intel IPP and blue represent the compound expression.

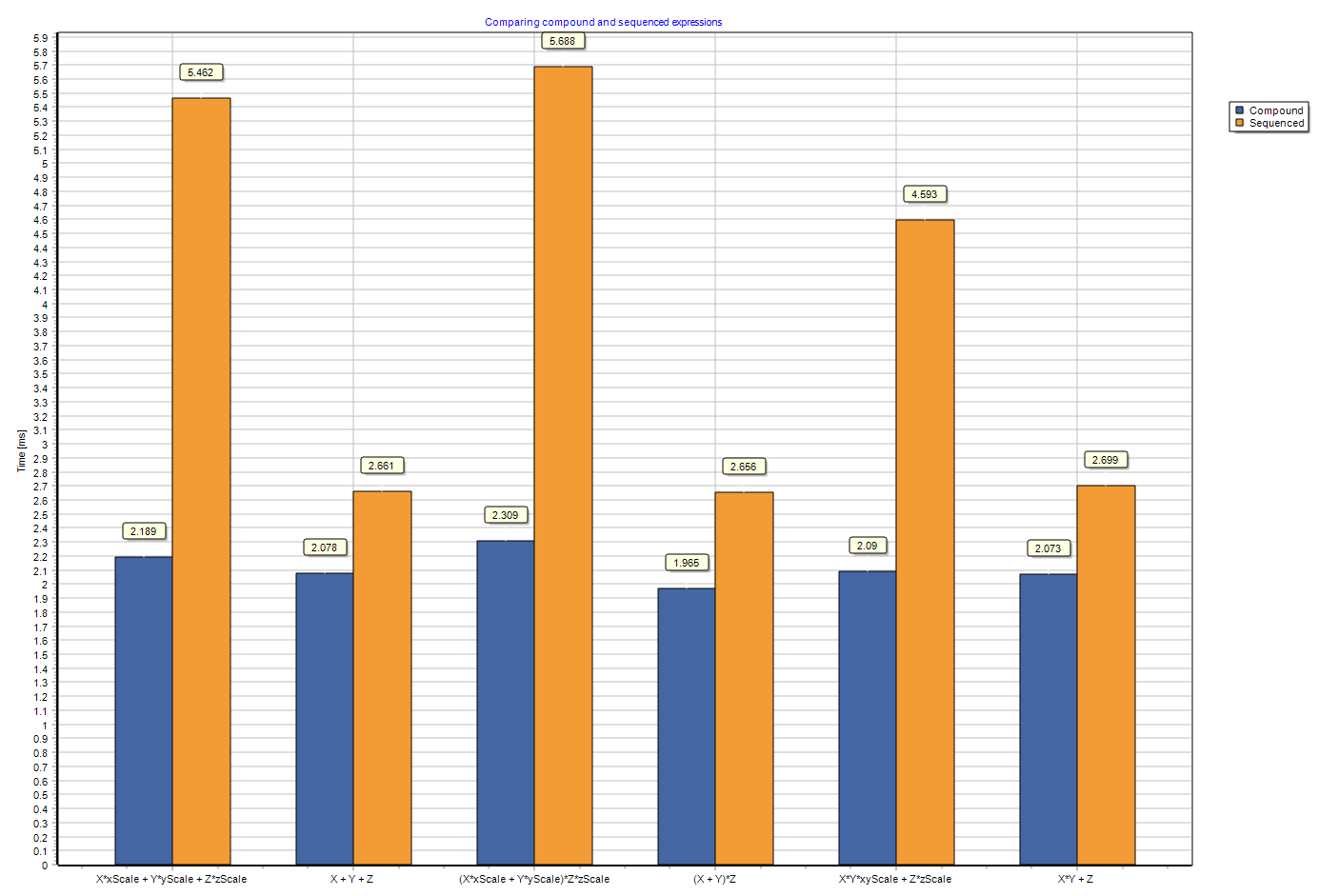
RomeZen2_3.2GHz_Compound.png

For Skylake AVX512 architecture, the advantage is not so much, but still present:

SkylakeAVX512_4GHz_Compound.PNG

The performance advantage varies depending on the CPU architecture quite considerably. Especially it makes sense to mix vectors with scalar operations, because such simple math expressions are limited mostly by memory bandwidth, which the scalar operations are not using. The following patterns have been made available, where X, Y and Z are vectors and the rest are scalars:

By passing the same parameters for Y or Z as for X in to the above methods the following (squared) expressions are also supported:

  • (sqr(X)*xScale + X*Y*yScale) *zScale
  • (sqr(X)*xScale - X*Y*yScale) *zScale
  • sqr(X)*Z*xyzScale
  • sqr(X)*xyScale + Z*zScale
  • sqr(X)*xyScale - Z*zScale
  • sqr(X)/Z*xyzScale
  • X / sqr(Y)*xyzScale

Plus all combinations with reductions, where the scalars are either equal to 1 or 0 for all of the above.  It is interesting to observe, that the following three examples:

  • X + Y
  • X*xScale + Y*yScale
  • X*xScale + Y*yScale, and finding min and max of the resulting vector

take the same amount of time. It makes sense therefore to find patterns in your code, which can take advantage of this. Or simply build algorithms which counter intuitevly would be slower, because they compute more, but are in fact faster. 

Compound expressions for integers

From including MtxVec v6.3.4 support for compound expressions using saturated integer math is also available. All the expressions listed before above will be evaluated at double the bit precision of its target storage. Integer will be omputed with 64bit precision and clamped to 32bit range before being stored. Provided, that the Int64 bit range is not exceeded during computation, it is possible to perform math with this extended range. For 16bit signed integers like smallInt, the computation is performed with 32bit precision and similarly for 8bit unsigned integer, it is performed at 16bit signed range. This gives us the possibility to run the computation at a higher bit range, deliver clamping before storing and still be faster, than alternative:

 

 IntegerCompound.PNG

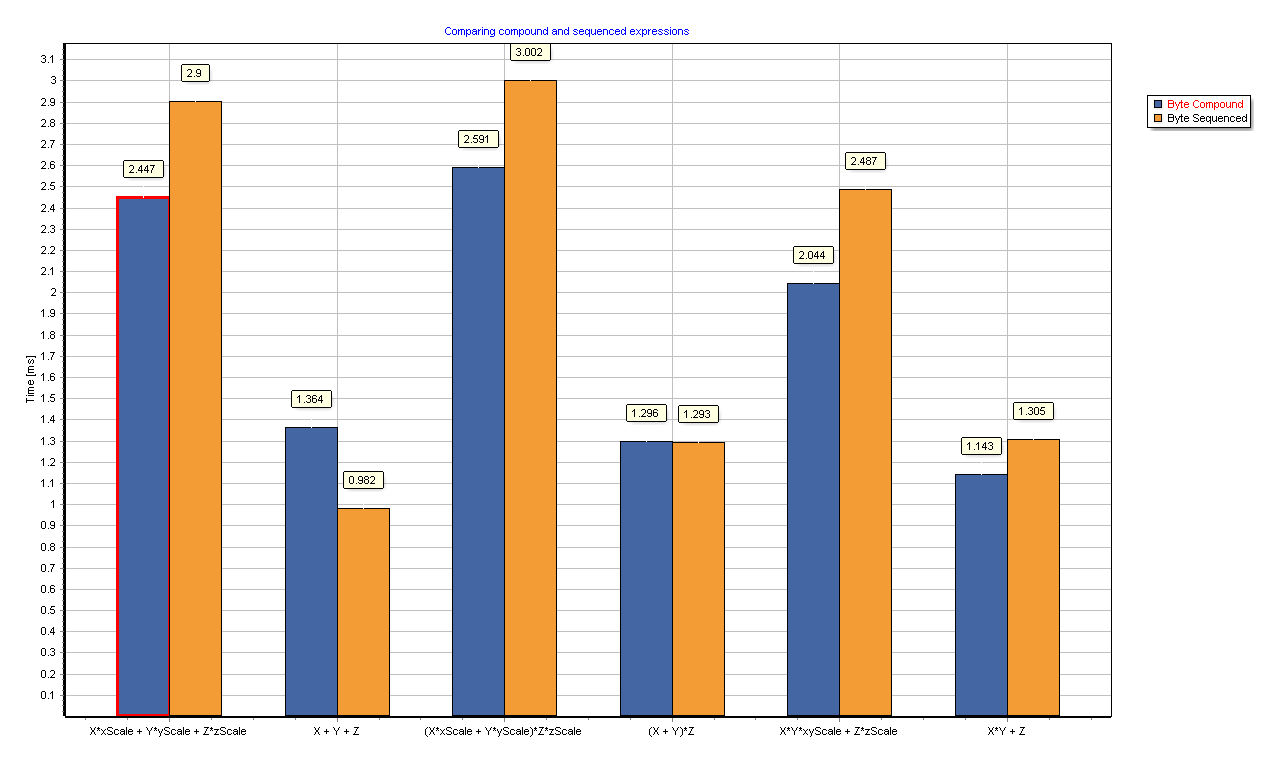
Over 160 routines to perform these computations are available as methods of TVecInt/TMtxInt/VectorInt/MatrixInt and also as global functions in the MtxExprInt unit. The improvements visible above are against Intel IPP which is an already very optimized library. 64bit delphi code for naive 32bit integer math (without saturation math and without intermediate results at higher precision) is at least 3x slower than IPP. When running with byte precision:

ByteCompound.PNG

The advantage is not so much, but there are also nearly no penalties. Note that the 8bit byte math is 3-5x faster than the 32bit integer. All the benchmarks on this page are a part of MtxVec Examples and are also installed with the trial version.