MtxVec - Under the hood
MtxVec is an object oriented vectorized math library, the core of Dew Lab Studio, featuring a comprehensive set of mathematical and statistical functions executing at impressive speeds.
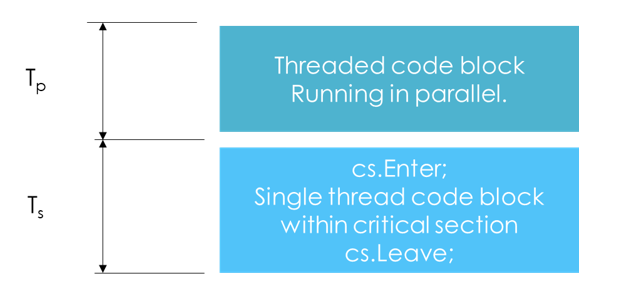
Fair Critical Section
A critical section is fair, if all threads entering a critical section exit in the same order in which they arrived.
Every time a thread enters sleep to wait, the sleeping time can be slightly different from thread to thread. The same variable time situation happens when the kernel is switching between threads (thread context switch). This non-determinism results in dice-throwing-like decision making process about which thread will enter next. A special design is required to guarantee that all threads are passed through the critical section in the order in which they arrived.
The problem develops when the number of threads waiting in the critical sections "Enter" waiting lock increases to "large" numbers. This happens, when most of the time spent by the algorithm is spent within the single threaded block of code, rather than in the multi-threaded block of code:
There can be different scenarios, where the queue of threads inside of the cs.Enter becomes large.
Performance degradation for unfair critical sections
If the critical section is not fair, a performance penalty of 2-3x for 16 core CPUs can sometimes be observed. This penalty grows with increasing CPU core count. The performance is also expected to vary considerably from run to run due to the dice throwing (random) nature of threads passing the Enter lock.
The primary cause of the performance degradation is that some threads remain stuck in the waiting loop of the critical sections Enter lock, while other threads may pass this lock multiple times. This can result in
- The CPU is underutilized, because not all CPU cores are used even though sufficient threads have been launched.
- Because some threads are stuck in the waiting loop, others cannot continue until they obtain the processing results of those which are stuck.
Implementation of a fair critical section
Although this code is open source, the license remains commercial and is included with the MtxVec Math library.
Brute-force exact KNN
K-NN or K nearest neighbors, is the grandfather of AI algorithms. It has many excellent properties, but one major flaw, the speed. With our implementation we accelerate KNN to performance levels not imaginable before. For very large problems (1M vectors compared with 1M vectors), the speed-up factor reaches 1000-2000x in compare to a naïve implementation on CPUs.
Once the performance of KNN is fixed, this opens up a whole array of applications, for which KNN was not considered interesting before. KNN was recently popularized by tSNE algorithm, which internally relies on KNN.
To open up the playing field, where KNN could be useful, let’s have a look at some numbers:
- 950k x 950k, 30 elements in vector, K = 50, 8x3.5GHz Skylake with AVX512, single precision takes 78s. With K = 1, 73s.
- 950k x 950k, 30 elements in vector, K = 50, 8x3.5GHz Skylake with AVX512, double precision takes 168s.
- Achieves linear scaling with core count and is thus faster than KD-Tree implementations for large problems.
- Price/performance advantage for CPU over GPU is more than 4x for double precision math. And it is simple and easy to deploy on CPU.
- Works equally well for symmetric and non-symmetric cases. The compare-to matrix can be different from the data matrix.
- It can use the same AI hardware, which is used to accelerate Deep Neural Networks, for acceleration.
- In the special case of K = 1 and assuming that all vectors contain quality data, KNN defeats DNN in accuracy with guaranteed and easily debugable results.
Current constraints:
- Only the Euclidian norm for the distance is possible.
- There is multi-threading support only down the “compare-to-data” dimension. If you are comparing only one vector to the previous dataset, only one CPU core will be used. However, to solve 950k x 1, 30 elements in vector, K = 50, 1x4GHz Skylake, takes 30ms.
The algorithm is called ClusteredKNN and is located in the MtxForLoop unit.
Multi-precision code
The main advantage of using single precision in compare to double, is to halve the memory usage and to double the speed of execution. The major new feature of MtxVec v6 is the capability to select algorithm precision at runtime. When a vector or matrix variable is declared and then sized for the first time:
a.Size(10, TMtxFloatPrecision.mvDouble);
You can optionally specify the storage precision. This storage precision can also be set/read with a property:
a.FloatPrecision
When working with the vector/matrix in expressions, the precision is preserved:
b.Sin(a);
This capability allows:
- User specified computational precision from the UI of your application.
- Write initial algorithm in any precision and decide on what is really needed after profiling.
Internally MtxVec will not strictly use only single precision, when the source data is in single precision. However, floating precision conversion is an expensive operation and it will try to avoid anything that might proove to be costly. At the same time, it will not unneccessarily drop the computational precision from double to single, when there is no performance or storage size benefit to be expected. This gives the user the best of both worlds.
For the source code users, it is possible to specify individual external libraries which are to be linked in. These libraries are available separately for single and for double precision floating point computation. If either precision is not used or needed, they can be left out from the distribution of the final application reducing the final package size.
When writing code, which can work with either single or double precision, consider that:
- The default array property or the indexer for an object a[i], will work with double or single precision of "a" Vector, but there will be some conversion cost, when the storage precision will be single. This coding pattern is meaningfull, when code simplicity helps, but does not affect the performance too much, because it is not used within tight loops.
- When tight loops are used and performance matters, it is recommend to split the branch between double and single (float) precision by checking the value of:
a.IsDouble
and access:
a.Values[i]
for double precision and
a.SValues[i]
for single precision.
Of course, the corresponding properties/values are available also for the complex number flavors:
a.CValues[i]
for double precision and
a.SCValues[i]
for single precision.
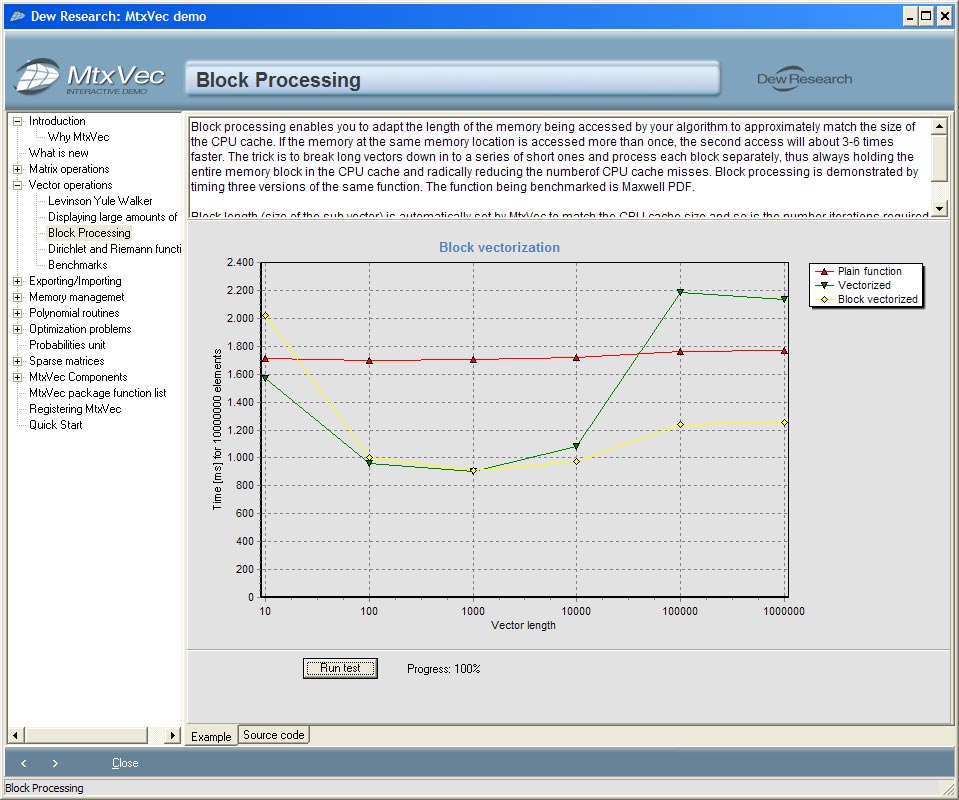
Block processing
Second step of code optimization after applying code vectorization is called block processing

Math functions and speed
MtxVec includes vectorized functions working on complex and real numbers

Super conductive memory manager
The way to massively parallel computation
The vector and matrix objects provided by MtxVec have the ability to be super conductive for multiple threads. This means that when multiple objects are allocated and freed from multiple threads, there will never be a case of contention, or synchronization lock. This allows multi-threaded applications to use MtxVec expressions like a + b without worrying about memory allocation bottlenecks. Without MtxVec such expressions can result in nearly 100% contention of threads. We benchmarked the evaluation speed of the following function by varying the size of input vectors:
function TestFunction(x,m,b: TVec): Vector;
var xm: Vector;
begin
xm.Adopt(x); //adopted by Vector to allow use of expressions
Result := 0.5*(1.0+ sgn(xm-m)*(1.0-Exp(-Abs(xm-m)/b)));
end;
The memory management features:
- Dedicated memory allocated per thread typically does not exceed CPU cache size (2MB). This makes the operation very memory and CPU cache efficient.
- MtxVec memory management does not interfere with other parts of the application which continue to use the default memory manager. Only those parts of code using MtxVec based vector/matrix objects are affected.
- Inteligent memory reuse keeps the working set of memory tightely packed and small, taking optimal advantage of the CPU cache design.
- Truly linear scaling of code on multiple cores becomes a reality.
The first picture shows an example of using two cores and comparing processing gains of super conductive memory manager with standard memory manager as a function of vector length:
As the number of cores increases the minimum vector length for which performance penalty is miniscule increases. As the vector length increases, the pressure on CPU cache size increases, thus possibly nullifying any gains due to multi-threading. By using MtxVec these problems can be completely avoided and fully linear scaling can be achieved independently of vector length. The second picture was done on a quad core CPU:
On quad core CPU, the differences increase showing a larger advantage, indicating that the default memory manager does not scale beyond two cores for this type of processing and that for short vectors the gains of using more than two cores can also be negative. (Gain factor larger than 4).
The source code of the benchmark is included with Dew Lab Studio trial version and Dew Lab Studio demos.

MtxVec expressions
It was Delphi 2006 that first introduced the ability to overload operators on records. This feature enabled MtxVec to add high performance support for using vectors, matrices and complex numbers in expressions.