MtxVec includes vectorized functions working on complex and real numbers

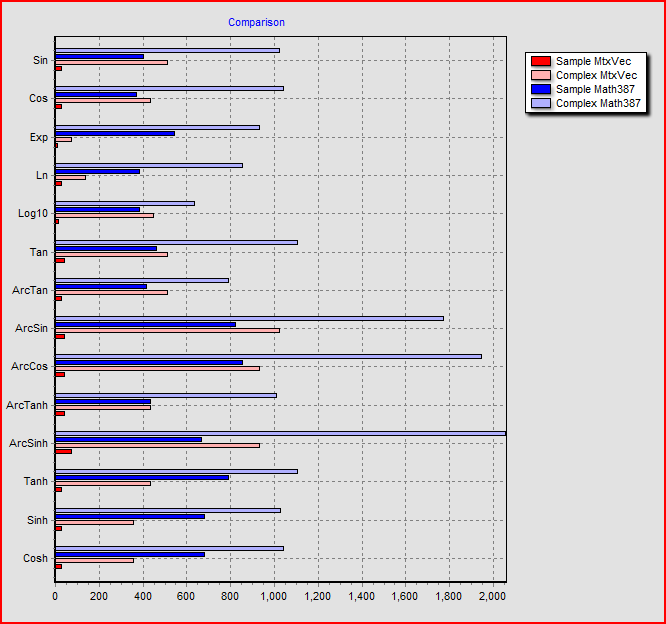
MtxVec math library includes basic complex math functions like sin, cos, tan, atan... whose performance is exceptional. Below are comparison charts between single value real number function version (Math387), single complex number function version (Math387), vectorized real number function version (MtxVec) and vectorized complex number function version (MtxVec). The single value real and complex number functions are written in assembler and use FPU. The vectorized versions of the same functions use SSE2/SSE3 instruction sets where possible. The benchmarks were ran on Pentium M 1.7GHz and Q6600. Tests on other CPU's show largely similar pattern.

Pentium M 1.7Ghz, MKL v9, MtxVec complex functions, vector length 4000 double precision elements.

The timing on the bottom Axis is in miliseconds. The length of the vectors tested is 1000 elements and number of iterations is 3000. Below is the timing of the same functions, but this time the complex vectorized math functions are from Intel MKL v9.1. In the chart legend they are still labeled as "Complex MtxVec".

Pentium M 1.7Ghz, MKL v9.1, MKL complex functions, vector length 4000 double precision elements.

Notice that bottom axis scales are different and that MKL complex number math is much slower. Vectorized complex number math functions from MtxVec maintain very high precision.

Intel Q6600, running MKL v10, threaded complex functions (EP), vector length 8000 double precision elements.

MtxVec runs substantially faster in all cases except in case of Exp and Ln functions which profit greatly from four cores in this case. In a two core case MtxVec is still faster.

Intel Q6600, running MKL v10, MtxVec complex functions (EP), vector length 8000 double precision elements.

The Benchmark code is public and is included in MtxVec demo app, which can be downloaded here. The trial version is found on the same page.