You are here: Symbol Reference > Optimization Namespace > Functions > Optimization.MinBrent Function
|
MtxVec VCL
|
Optimization.MinBrent Function
|
MtxVec VCL
|
Minimizes single variable function.
|
Parameters |
Description |
|
ax |
Defines initial lower limit for minimum search. |
|
bx |
Defines initial uššer limit for minimum search. |
|
Func |
Real functin of single variable (must be of TRealFunction type) to be minimized. |
|
FloatPrecision |
Specifies the floating point precision to be used by the routine. |
|
Consts |
Additional Fun constant parameters (can be/is usually nil). |
|
ObjConst |
Additional Fun constant parameters (can be/is usually nil). |
|
MinX |
Returns the position of function minimum. |
|
MaxIter |
Maximum allowed numer of minimum search iterations. |
|
Accuracy |
Desired minimum position tolerance. |
|
Verbose |
If assigned, stores Func, evaluated at each iteration step. Optionally, you can also pass TOptControl object to the Verbose parameter. This allows the optimization procedure to be interrupted from another thread and optionally also allows logging and iteration count monitoring. |
the number of iterations required to reach the solution(minimum) within given tolerance.
Minimizes the function of one variable. This routine uses slightly modified version of the algol 60 procedure localmin, introduced by Richard Brent.
Problem: Find the minimum of the function of single variable by using the Brent method.
Solution:The function is defined by the following equation:
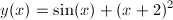
|
Copyright (c) 1999-2025 by Dew Research. All rights reserved.
|
What do you think about this topic? Send feedback!
|