You are here: Symbol Reference > Optimization Namespace > Functions > Optimization.MinBrent Function
Problem: Find the minimum of the function of single variable by using the Brent method.
Solution:The function is defined by the following equation:
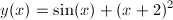
|
Copyright (c) 1999-2025 by Dew Research. All rights reserved.
|