Statistics

By definition the covariance matrix is a matrix of covariances between elements of a vector. It is the natural generalization to higher dimensions of the concept of the variance of a scalar-valued random variable. 

If X columns represent observation samples (variables), it's rows sample(s) values (observables), mu_j X_j j-th column average value, then the covariance matrix is defined as: 

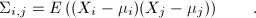
or in matrix form: 

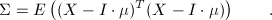
where E is the expected value. The inverse of this matrix, is called the inverse covariance matrix or the precision matrix.

This version does all necessary calculations to calculate covariance matrix.

Functions