Statistics

X and Y can be two vectors or matrices of equal size. In first case two vectors are treated as two variables, X values as first variable observables, Y vector values as second variable observabled. In second case two matrices are treated as two variables X and Y, all X values as X variable observables and all Y values as Y variable observables.

For column-vector valued random variables X and Y with respective expected values mu and nu, and respective scalar components m and n, the covariance is defined to be the m×n matrix called the covariance matrix: 

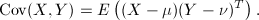
Calculate the covariance matrix from two vectors representing two variables.

var Data1, Data2: Vector;
  CovMtx : Matrix;
begin
  Data1.SetIt(false,[1.2,3]);
  Data2.SetIt(false,[5,5.5]);
  Covariance(Data1,Data2,CovMtx,False);
    // cov = [1.62, 0.45,
    //        0.45, 0.125]
end;

#include "MtxExpr.hpp"
#include "Statistics.hpp"
void __fastcall Example()
{
    sVector data1,data2;
    sMatrix cov;
    data1.SetIt(false,OPENARRAY(double,(1.2,3)));
    data2.SetIt(false,OPENARRAY(double,(5,5.5)));
    Covariance(data1,data2,cov,false);
    // cov = [1.62, 0.45,
    //        0.45, 0.125]
}

Functions