Optimization.ConjGrad Function

Minimizes the function of several variables by using the Conjugate gradient optimization algorithm.

Pascal

function ConjGrad(Fun: TRealFunction; Grad: TGrad; var Pars: Array of double; Const Consts: array of double; Const ObjConst: Array of TObject; out FMin: double; out StopReason: TOptStopReason; const FloatPrecision: TMtxFloatPrecision; FletcherAlgo: Boolean = true; SoftLineSearch: boolean = true; MaxIter: Integer = 500; Tol: double = 1.0E-8; GradTol: double = 1.0E-8; const Verbose: TStrings = nil): Integer; overload;

File

Optimization

Parameters

Parameters	Description
Fun	Real function (must be of TRealFunction type) to be minimized.
Grad	The gradient and Hessian procedure (must be of TGrad type), used for calculating the gradient.
Pars	Stores the initial estimates for parameters (minimum estimate). After the call to routine returns adjusted calculated values (minimum position).
Consts	Additional Fun constant parameteres (can be/is usually nil).
ObjConst	Additional Fun constant parameteres (can be/is usually nil).
FMin	Returns function value at minimum.
StopReason	Returns reason why minimum search stopped (see TOptStopReason).
FloatPrecision	Specifies the floating point precision to be used by the routine.
FletcherAlgo	If True, ConjGrad procedure will use Fletcher-Reeves method. If false, ConjGrad procedure will use Polak-Ribiere method.
SoftLineSearch	If True, ConjGrad internal line search algoritm will use soft line search method. Set SoftLineSearch to true if you're using numerical approximation for gradient. If SoftLineSearch if false, ConjGrad internal line search algorithm will use exact line search method. Set SoftLineSearch to false if you're using exact gradient.
MaxIter	Maximum allowed numer of minimum search iterations.
Tol	Desired Pars - minimum position tolerance.
GradTol	Minimum allowed gradient C-Norm.
Verbose	If assigned, stores Fun, evaluated at each iteration step. Optionally, you can also pass TOptControl object to the Verbose parameter. This allows the optimization procedure to be interrupted from another thread and optionally also allows logging and iteration count monitoring.

Returns

the number of iterations required to reach the solution(minimum) within given tolerance.

Example

Problem: Find the minimum of the "Banana" function by using the Conjugate gradient method.

Solution:The Banana function is defined by the following equation:

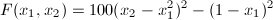
Normally ConjGrad method would also require gradient procedure. But in this example we'll use the numerical approximation, more precisely the MtxIntDiff.NumericGradRichardson routine. This is done by specifying NumericGradRichardson routine as Grad parameter in ConjGrad routine call (see below)

Uses MtxVec, Math387, Optimization; function Banana(const Pars: TVec; const Consts: TVec; const OConsts: array of TObject): double; begin Banana := 100*Sqr(Pars[1]-Sqr(Pars[0]))+Sqr(1-Pars[0]); end; procedure Example; var Iters : integer; Pars: array [0..1] of double; StopReason: TOptStopReason; begin // initial estimates for x1 and x2 Pars[0] := 0; Pars[1] := 0; Iters := ConjGrad(Banana,NumericGradRichardson,Pars,[],[],FMin,StopReason,mvDouble,IHess); //stop if Iters > 500 or Tolerance < 1e-8 // Returns Pars = [1,1] and FMin = 0, meaning x1=1, x2=1 and minimum value is 0 end;

#include "MtxExpr.hpp" #include "Math387.hpp" #include "Optimization.hpp" #include "MtxIntDiff.hpp" // Objective function double __fastcall Banana(TVec* const Parameters, TVec* const Constants, System::TObject* const * ObjConst, const int ObjConst_Size) { double* Pars = Parameters->PValues1D(0); return 100.0*IntPower(Pars[1] - IntPower(Pars[0],2),2) + IntPower(1.0 - Pars[0],2); } void __fastcall Example(); { double Pars[2]; double fmin; TOptStopReason StopReason; // initial estimates for x1 and x2 Pars[0] = 0; Pars[1] = 0; int iters = ConjGrad(Banana, NumericGradRichardson,Pars,1,NULL,-1,NULL,-1,fmin, StopReason, mvDouble, true,false,1000,1.0e-8,1.0e-8,NULL); // stop if Iters >1000 or Tolerance < 1e-8 }

Optimization, Functions, Example, See Also

What do you think about this topic? Send feedback!