Minimizes the function of several variables by using the Quasi-Newton optimization algorithm.
|
Parameters |
Description |
|
Fun |
Real function (must be of TRealFunction type) to be minimized. |
|
Grad |
The gradient and Hessian procedure (must be of TGrad type), used for calculating the gradient. |
|
Pars |
Stores the initial estimates for parameters (minimum estimate). After the call to routine returns adjusted calculated values (minimum position). |
|
Consts |
Additional Fun constant parameteres (can be/is usually nil). |
|
ObjConst |
Additional Fun constant parameteres (can be/is usually nil). |
|
FMin |
Returns function value at minimum. |
|
IHess |
Returns inverse Hessian matrix. |
|
StopReason |
Returns reason why minimum search stopped (see TOptStopReason). |
|
FloatPrecision |
Specifies the floating point precision to be used by the routine. |
|
DFPAlgo |
If True, BFGS procedure will use Davidon-Fletcher-Powell Hessian update scheme. If False, BFGS procedure will use Broyden-Fletcher-Goldberg-Shamo Hessian update scheme. |
|
SoftLineSearch |
If True, BFGS internal line search algoritm will use soft line search method. Set SoftLineSearch to true if you're using numerical approximation for gradient. If SoftLineSearch if false, BFGS internal line search. algorithm will use exact line search method. Set SoftLineSearch to false if you're using *exact* gradient. |
|
MaxIter |
Maximum allowed numer of minimum search iterations. |
|
Tol |
Desired Pars - minimum position tolerance. |
|
GradTol |
Minimum allowed gradient C-Norm. |
|
Verbose |
If assigned, stores Fun, evaluated at each iteration step. Optionally, you can also pass TOptControl object to the Verbose parameter. This allows the optimization procedure to be interrupted from another thread and optionally also allows logging and iteration count monitoring. |
the number of iterations required to reach the solution(minimum) within given tolerance.
Problem: Find the minimum of the "Banana" function by using the BFGS-DFP method.
Solution:The Banana function is defined by the following equation:
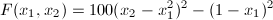
Also, BFGS method requires the gradient of the function. The gradient of the Banana function is:
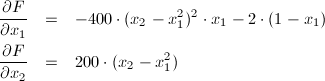
|
Copyright (c) 1999-2025 by Dew Research. All rights reserved.
|
What do you think about this topic? Send feedback!
|