Performs a singular value decomposition on a calling matrix (A). U or V can be nil, if not desired. If you do not want economy size U and V set MinSize to False. The singular value decomposition (SVD) of the calling matrix (A, with m rows and n cols) is defined by the following equation: 

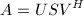
where U and V are unitay (for complex A) or orthogonal (for real A). S is a diagonal matrix with real diagonal elements is: 

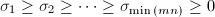
The diagonal elements are singular values of A (calling matrix). The first min(m, n) columns of the matrices U and V are, respectively, left and right singular vectors of calling matrix (A). The singular values and singular vectors satisfy: 

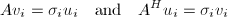
where u_i and v_i are the i-th columns of U and V, respectively. One interpretation of the singular values is as follows. If you take a unit sphere in n-dimensional space, and multiply each vector in it by an m x n matrix , you will get an ellipsoid in m-dimensional space. The singular values give the lengths of the principal axes of the ellipsoid. If the matrix is singular in some way, this will be reflected in the shape of the ellipsoid. In fact, the ratio of the largest singular value of a matrix to the smallest one gives a ConditionNr of the matrix, which determines, for example, the accuracy of numerical matrix inverses. Very small singular values are usually numerically meaningless.

SVDSolve, ConditionNr

SVD Method