Statistics.MDScaleStress Function

The stress factor for multidimensional scaling.

Pascal

function MDScaleStress(const D: TMtx; const DHat: TMtx): double;

File

Statistics

Parameters

Parameters	Description
D	Data distance matrix.
DHat	Estimated distance matrix.

Returns

The stress factor.

Description

Calculates the GOF statistics for multidimensional scaling. The stress factor is defined as:

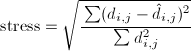
where hat(d(i,j)) is the predicted distance based on the MDS model. In his original paper on multi dimensional scaling, Kruskal (1964) gave following advise about stress values based on his experience:

Stress	Goodness-of-fit
0.2	poor
0.1	fair
0.05	good
0.025	excellent
0.000	perfect

More recent articles caution against using a table like this since acceptable values of stress depends on the quality of the distance matrix and the number of objects in that matrix.

See Also

MDScaleMetric

Example

D stores data distance matrix, DHat stores reduced dimension estimated distance matrix.

Uses MtxExpr, Statistics, Math387;
procedure Example;
var D,DHat: Matrix;
  stress: double;
begin
  D.Size(2,2,false,[0,1,2,3]);
  DHat.Size(2,2,false,[0.1,1.2,2.5,3]);
  // Calculate stress value - measure for GOF
  // Smaller stress value means better GOF.
  stress := MDScaleStress(D,DHat);
end;

#include "MtxExpr.hpp"
#include "Statistics.hpp"
void __fastcall Example()
{
    sMatrix D,DHat;
    D.SetIt(2,2,false, OPENARRAY(double, (0,1,2,3)));
    DHat.SetIt(2,2,false, OPENARRAY(double, (0.1,1.2,2.5,3)));

    // Calculate stress value - measure for GOF
    // Smaller stress value means better GOF.
    double stress = MDScaleStress(D,DHat);
}

Statistics, Functions, Example, See Also

What do you think about this topic? Send feedback!