Statistics.AndersonDarling Function

Anderson-Darling GOF test.

Pascal

function AndersonDarling(const Data: TVec; Distribution: TDistribution; out hRes: THypothesisResult; out Signif: double; Alpha: double = 0.05): double;

File

Statistics

Parameters

Parameters	Description
Data	Stores ordered data.
Distribution	Perform test for this distribution. Supported distributions : exponential, log-normal, normal and weibull.
hRes	Returns the result of the null hypothesis.
Signif	(Significance level) returns the probability of observing the given result by chance given that the null hypothesis is true.
Alpha	Defines the desired significance level. If the significance probability (Signif) is bellow the desired significance (Alpha), the null hypothesis is rejected.

Returns

Anderson-Darling test statistics, adjusted with small sample size factor.

Description

The Anderson-Darling test (Stephens, 1974) is used to test if a sample of data came from a population with a specific distribution. It is a modification of the Kolmogorov-Smirnov (K-S) test and gives more weight to the tails than does the K-S test. The K-S test is distribution free in the sense that the critical values do not depend on the specific distribution being tested. The Anderson-Darling test makes use of the specific distribution in calculating critical values. This has the advantage of allowing a more sensitive test and the disadvantage that critical values must be calculated for each distribution.

The Anderson-Darling test is defined as:

H0: The data follow a specified distribution.
Ha: The data do not follow the specified distribution.

The test statistics is defined as:

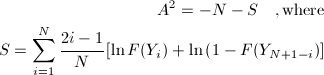
where F is the cumulative distribution function of distribution being tested.

To learn more about A-D test, check the following links:

hrefhttp://www.itl.nist.gov/div898/handbook/eda/section3/eda35e.htmhttp://www.itl.nist.gov/div898/handbook/eda/section3/eda35e.htm
hrefhttp://Src.alionscience.com/pdf/A_DTest.pdfhttp://Src.alionscience.com/pdf/A_DTest.pdf

Note

The basic assumption is that the data values are sorted in ascending order.