You are here: Symbol Reference > Probabilities Namespace > Functions > Probabilities.RiemannZeta Function
Riemann Zeta function.
|
Parameters |
Description |
|
Z |
Defines complex value for which the Riemann zetao function is to be calculated. |
|
n |
Defines used number of terms used in complex series approximation of Riemann zeta function. |
the Riemman zeta function.
The Riemann zeta-function is the function of a complex variable z initially defined by the following infinite series:
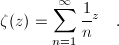 ,
,
for values of z with real part greater than one, and then analytically continued to all complex z <> 1. The zeta-function satisfies the following functional equation:
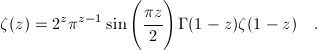 ,
,
valid for all complex numbers z. Zeta function is related to Dirichlet Lambda and Eta functions by:
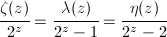
|
Copyright (c) 1999-2025 by Dew Research. All rights reserved.
|
What do you think about this topic? Send feedback!
|