You are here: Symbol Reference > Probabilities Namespace > Functions > Probabilities.NormalCDFInv Function
Normal distribution point percent function (PPF).
|
Parameters |
Description |
|
p |
Probability, real positive value on closed interval [0,1]. |
|
Mu |
Distribution location parameter, real value. |
|
sigma |
Distribution scale parameter, real positive value. |
the normal distribution point percent function (PPF) for probability p using the parameters Mu (mean value) and sigma (standard deviation). Probability p must lie on the interval [0,1] and sigma must be positive value, otherwise the result is NAN.
function NormalCDF(x, Mu, sigma: single): single; overload;
The normal distribution point percent function is defined by the following equation:
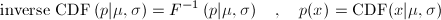
where Mu is mean value and sigmsa is standard deviation. The result of NormalCDFInv is the solution of the integral equation above with the parameters Mu and sigma where you supply the probability p.
|
Copyright (c) 1999-2025 by Dew Research. All rights reserved.
|
What do you think about this topic? Send feedback!
|