Probabilities.HypGeometricCDF Function

Hypergeometric cumulative distribution function (CDF).

Pascal

function HypGeometricCDF(x: Integer; M: Integer; K: Integer; N: Integer): double; overload;

Parameters	Description
x	Distribution domain, integer on closed interval [0,N].
M	Defines total number of elements, valid values ae integers on closed interval [0,X].
K	Defines number of elements with certain traits, valid values are integers on closed interval [X,M].
N	Defines number of samples, valid values are integers on closed interval [X,M].

Returns

the hypergeometric cumulative distribution function (CDF) for value x using the integer parameters M (total number of elements), K (number of elements with a certain trait) and N (number of samples drawn). Value x must be greater of equal than zero, all the parameters M, K N must be greater or equal than zero, M >= N, M >= K, N >= X, K >= x. If not all of these conditions are met, the result is NAN.

Description

function HypGeometricPDFs(x: Integer; M, K, N: Integer): single; overload;

The hypergeometric cumulative distribution function is defined by the following equation:

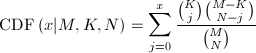
The result of HypGeometricCDF is the probability of drawing up to x elements of a possible K in N drawings without replacement from a group of M elements.