Probabilities.ChiSquarePDF Function

Chi-squared probability density Function (PDF).

Pascal

function ChiSquarePDF(x: double; Nu: Integer): double; overload;

Parameters	Description
x	Function domain, real positive value.
Nu	Defines distribution degrees of freedom. Nu must be a positive integer value.

Returns

the Chi-squared probability density Function (PDF).

Description

Calculates the Chi-Squared probability density function, defined by the following equation:

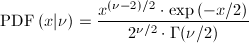
where n (Nu) is the degrees of freedom and G is Math387.Gamma function. One of the most important classes of quadratic functions in sampling theory is the class of functions reducible to sums of squares of Nu independent standard normals. This function is called a chi-squared function with Nu degrees of freedom. A chi-squared random variable is completely specified by stating its degrees of freedom Nu. The chi-squared distribution is just a special case of GammaPDF distribution (for gamma distribution parameter b=2).