Probabilities.BinomPDF Function

Binomial probability density function (PDF).

Pascal

function BinomPDF(x: Integer; N: integer; p: double): double; overload;

Parameters	Description
x	Function domain, integer, valid on closed interval [0,n].
N	Defines number of trials. n must be a positive integer.
p	Defines success probability. p must lie on the [0,1] closed interval.

Returns

the binomial probability density function (PDF).

Remarks

Calculates the binomial probability density function. The binomial probability density function is defined by the following equation:

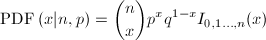
where q=1-p and I is the discrete interval [0,1,...n] on which the binomial CDF is not zero. The result of BinomPDF is the probability of observing x successes in n independent trials and where the probability of success in any given trial is p.

To recognize a situation that involves a binomial random variable, following assumptions must be met:

The experiment consists of a fixed number, n, of Bernoulli trials that result in either success or failure.
The trials are identical and independent and therefore the probability of success p, remains the same from trial to trial.
The random variable x denotes the number of successes obtained in the n trials.