Probabilities.BetaPDF Function

Beta probability density function (PDF).

Pascal

function BetaPDF(x: double; a: double; b: double): double; overload;

Parameters	Description
x	Function domain, real positive value on closed interval [0,1].
a	Shape parameter, real positive value.
b	Shape parameter, real positive value.

Returns

the beta distribution probability density function (PDF).

Description

Calculates the beta probability density function. The beta probability density function is defined by the following equation:

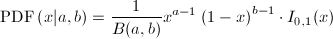
where B(a,b) is Beta function and it defines the interval on which the beta PDF is not zero. The beta distribution describes a family of curves that are nonzero only on the interval [0,1]. The parameters a and b must both be greater than zero and x must lie on the interval (0,1) otherwise the result is NAN.

See Also

BetaCDF, BetaCDFInv

Example

Calculate Beta distribution (a=3 and b= 2.1) PDF and CDF for x =0.55

Uses Probabilities; procedure Example; var pdf,cdf: double; begin pdf := BetaPDF(0.55, 3.0, 2.1); cdf := BetaCDF(0.55, 3.0, 2.1); end;

#include "Probabilities.hpp" void __fastcall Example() { double pdf = BetaPDF(0.55, 3.0, 2.1); double cdf = BetaCDF(0.55, 3.0, 2.1); }

Probabilities, Functions, Example, See Also

What do you think about this topic? Send feedback!