Optimization.SimplexDual Function

Linear optimization by Dual Simplex algorithm.

Pascal

function SimplexDual(const A: TMtx; const b: TVec; const c: TVec; const AFinal: TMtx; const X: TVec; const Indexes: TVecInt; out SolutionType: TLPSolution; Minimize: boolean = true; const Verbose: TStrings = nil): double;

File

Optimization

Parameters

Parameters	Description
A	Defines initial values for A*x >= b relation.
b	Defines initial values for A*x >= b relation.
c	Defines values in f=c(T)*x equation.
AFinal	Returns the final tableaux.
X	Returns values of the legitimate variables (optimal solution).
Indexes	Returns indices (in IValues) of the basic variables in AFinal tableu.
SolutionType	Returns type of LP solution.
Minimize	If false, find minimum of the objective function f. If false, find maximum of the objective function f.
Verbose	If assigned, each tableu and row/column pivoting is logged to Verbose. Optionally, you can also assign TOptControl object to the Verbose parameter. This allows the optimization procedure to be interrupted from another thread and optionally also allows logging and iteration count monitoring.

Returns

Value of the objective function, evaluated at minimum or maximum.

Description

Solves the following optimization problem:

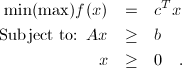
Components of the vector b are not required to satisfy the nonnegativity constraints. The Dual Simplex Algorithm has numerous applications to other problems of linear programming. It is used, for instance, in some implementations of the Gomory's cutting plane algorithm for solving the integer programming problems.

See Also

SimplexTwoPhase

Example

Solve linear programming problem with 3 equations and 4 positive constraints.

Uses Optimization, MtxExpr, Math387; procedure Example var A,Af: Matrix; b,c,x,indexes: Vector; f: double; sol: TLPSolution; begin A.SetIt(3,4,false,[2,1,5,0,1,2,3,0,1,1,1,1]); b.SetIt(false,[20,25,10]); c.SetIt(false,[1,2,3,-1]); // Find maximum using above system f := SimplexDual(A,b,c,Af,x,indexes,sol,false,nil); end;

#include "MtxExpr.hpp" #include "Math387.hpp" #include "Optimization.hpp" void __fastcall Example; { sMatrix A,Af; sVector b,c,x,indexes; TLPSolution sol; A.SetIt(3,4,false, OPENARRAY(double,(2,1,5,0,1,2,3,0,1,1,1,1))); b.SetIt(OPENARRAY(double,(20,25,10))); c.SetIt(OPENARRAY(double,(1,2,3,-1))); // Find maximum using above system double f = SimplexDual(A,b,c,Af,x,indexes,sol, false, NULL); }

Optimization, Functions, Example, See Also

What do you think about this topic? Send feedback!