Introduction:

Using MtxVec optimization routines you can with just few lines of code do unconstrained minimization, bounded minimization on scalar or vector function, all kinds of non-linear regressions, zero finding and even goal seeking (what-if) scenarios. This example deals with non-linear fit of function of at least two independent variables ( X1 and X2), three function parameters (k,A,B) and one dependent variabld, namely Z. This relation can be expressed in vector form as Z=Z(k,A,B| X1,X2). The "problem" with this model is we're used to one independent variable X1, but this model uses two variables and is described by the following relation:

The solution to the problem is to find the parametervalues k, A and B which, when insterted in the model equation yield the closest match to the experimental values Z(X1,X2). Below is shown the original measured dataset. Data was kindly provided by Mitch dot Barker at mt dot com.

In the graph above X1 and X2 are plotted against Z. Actual graphing was done using TeeChart v2 for .NET with a single line of code (TeeChart.DrawValues(new TVec[3] {x1,z,x2},tChart1.Chsrt.Series[0]);). Plotted data shows a distinctive power model in both directions.

Parameter initial estimates and boundary values

Boundary values can usualy be extracted from model itself. In our case k takes arbitrary real values and A,B are both positive real numbers. Likewise we can also use the model to get initial estimates for all parameters (see implementation below. Another approach to finding initial estimates is to use brute force to find parameter values which return the smallest RSS.

All this in mathematical terms translates to finding optimal values for k, A and B which minimize sum of squared differences betwen experimental and calculated Z values i.e sum of squared differences of residuals.

uses MtxExpr, Optimization, MtxVec, Math387;
   
// This is the objective function we're trying to minimize
// It is the Residuals Sum of Squares where the residuals are the
// difference betwen calculated and measured z values

function FVObjFun(Parameters: TVec; const Constants: array of TSample;
   OC: array of TObject): TSample;
var c,x,z,zcalc,res: Vector;
   k,a,b: double;
begin
   x := Vector(ObjConst[0]);
   y := Vector(ObjConst[1]);
   z := Vector(ObjConst[2]);
   zcalc := Vector(ObjConst[3]);
   res := Vector(ObjConst[4]);

   k := Parameters[0];
   a := Parameters[1];
   b := Parameters[2];
   // Calculated values
   res.Power(y, b);
   zcalc.Power(x, a);
   zcalc.Mul(res);
   zcalc.Mul(k);
   // Residuals
   res.Sub(zcalc, z);
   // RSS - we want to minimize this
   // minimizing square of difference, not difference
   Result := rea.SumOfSquares;
end;

procedure DoCalculation;
var stopReason: TOptStopReason;
   targetValue, rss: TSample;
   numper: Integer;
var c,x,z,zcalc,res: Vector;
   pars; array[0..] of TSample;
begin
   x.LoadFromFile('.\Data\x_data.vec');
   y.LoadFromFile('.\Data\y_data.vec');
   z.LoadFromFile('.\Data\z_data.vec');
   pars[0] := 0.1;
   pars[1] := 1;
   pars[2] := 1;
 
   Simplex(FVObjFun, pars, [x,y,z,.zcalc, res], nil, 
   [-INF,0.0, 0.0],0 [INF,0.0, 0.0],
   rss, stopReason, 500, 1e-4, nil);
end;       

using System;
using System.Collections.Generic;
using System.Text;
using Dew.Math;
using Dew.Math.Units;
namespace Dew.Examples
{
   class Program
   {
      // This is the objective function we're trying to minimize
      // It is the Residuals Sum of Squares where the residuals are the
      // difference betwen calculated and measured z values
      static double ObjFun(TVec Parameters, double[] Constants, params object[] ObjConst)
      {

         Vector x, y, z, zcalc, res;
         x = (Vector)ObjConst[0];
         y = (Vector)ObjConst[1];
         z = (Vector)ObjConst[2];
         zcalc = (Vector)ObjConst[3];
         res = (Vector)ObjConst[4];
         double k, a, b;
          
         k = Parameters[0];
         a = Parameters[1];
         b = Parameters[2];
         // Calculated values
         res.Power(y, b);
         zcalc.Power(x, a);
         zcalc.Mul(res);
         zcalc.Mul(k);
 

         // Residuals
         res.Sub(zcalc, z);
         // RSS - we want to minimize this
         return res.SumOfSquares();
      }

 
      static void DoCalculation()
      {
         Vector x, y, z, v1, v2;
         x = new Vector(0);
         y = new Vector(0);
         z = new Vector(0);
         x.LoadFromFile(@".\Data\x_data.vec");
         y.LoadFromFile(@".\Data\y_data.vec");
         z.LoadFromFile(@".\Data\z_data.vec");
         v1 = new Vector(0);
         v2 = new Vector(0);
 

         TOptStopReason stopReason;
         double rss;
         // Initial estimates from experiment
         double[] pars = new double[];
         pars[0] = 0.01; // k
         pars[1] = 1; // A
         pars[2] = 1; // B
         // Output to console
         Console.WriteLine("");
         Console.WriteLine("Non linear optimization - Case study 006 - C#");
         Console.WriteLine("Model z(k,A,B|X1,X2)=k*X1^A*X2^B\n"); 
         Console.WriteLine("Initial estimates for parameters:");
         Console.WriteLine("k:\t" + pars[0].ToString());
         Console.WriteLine("A:\t" + pars[1].ToString());
         Console.WriteLine("B:\t" + pars[2].ToString()+"\n");
         // Define lower and upper bounds for k,a and b
         // -INF < k < INF, 0 < a < INF, 0 < b < INF
         int num = Optimization.Simplex(ObjFun, ref pars, null,
         new object[] { x, y, z, v1, v2 },
         new double[3] { - Math387.INF, 0, 0 }, // Lower bounds
         new double[3] { Math387.INF, Math387.INF, Math387.INF }, // Upper bounds

         out rss, out stopReason, 500, 1.0E-8, null);


         Console.WriteLine("Number of iterations:\t" + num.ToString());
         Console.WriteLine("RSS:\t" + rss.ToString()+"\n");
         Console.WriteLine("k:\t" + pars[0].ToString());
         Console.WriteLine("A:\t" + pars[1].ToString());
         Console.WriteLine("B:\t" + pars[2].ToString()); 
         Console.WriteLine("----------------------------------------------");
         Console.Read(); 
      }
 
      static void Main(string[] args)
      {
         DoCalculation();
      }
   }
}

Using these values for initial estimates, Simplex algorithm returns optimal values after 138 iterations:

• k = 0.01000245
• A = 1.29972511
• B = 0.95026208
• RSS = 0.0000026570

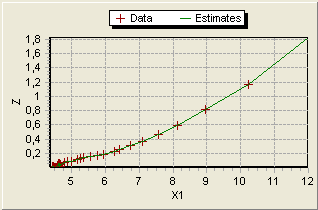
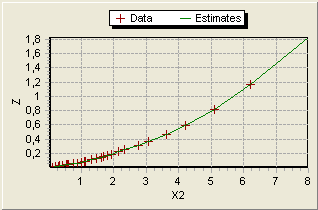
Projecting calculated values (green line) onto X1-Z and X2-Z plane reveals close match to measured data (red crosses).

Additional things to try:

• Try changing initial values for parameters.
• Use Marquardt and Trust Regiobn methods to find optimal values for k, A and B.