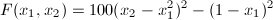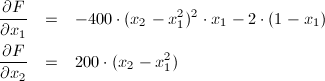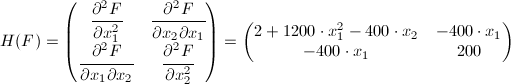#include "MtxExpr.hpp"
#include "Math387.hpp"
#include "Optimization.hpp"
// Objective function
double __fastcall Banana(
TVec*
const Parameters,
TVec*
const Constants, System::TObject*
const * ObjConst,
const int ObjConst_Size)
{
double* Pars = Parameters->PValues1D(0);
return 100.0*
IntPower(Pars[1]-
IntPower(Pars[0],2),2)+
IntPower(1.0-Pars[0],2);
}
// Analytical gradient and Hessian matrix of the objective function
void __fastcall BananaGradHess(
TRealFunction Fun,
TVec*
const Parameters,
TVec*
const Consts,
System::TObject*
const * ObjConst,
const int ObjConst_Size,
TVec*
const Grad,
TMtx*
const Hess)
{
double* Pars = Parameters->PValues1D(0);
Grad->Values[0] = -400*(Pars[1]-
IntPower(Pars[0],2))*Pars[0] - 2*(1-Pars[0]);
Grad->Values[1] = 200*(Pars[1]-
IntPower(Pars[0],2));
Hess->Values1D[0] = -400*Pars[1]+1200*
IntPower(Pars[0],2)+2;
Hess->Values1D[1] = -400*Pars[0];
Hess->Values1D[2] = -400*Pars[0];
Hess->Values1D[3] = 200;
}
void __fastcall Example();
{
double Pars[2];
double fmin;
TOptStopReason StopReason;
// initial estimates for x1 and x2
Pars[0] = 0;
Pars[1] = 0;
int iters = Marquardt(Banana,GradHessBanana,Pars,1,NULL,-1,NULL,-1,fmin, StopReason, mvDouble,
true,
false,1000,1.0e-8,1.0e-8,NULL);
// stop if Iters >1000 or Tolerance < 1e-8
}